Različita su shvatanja o tome koliko je kineska matematika uticala na matematike u starim civilizacijama Indije, Egipta, Mesopotamije,Grčke, a koliko su pak matematike tih civilizacija uticale na kinesku. Veze među starim narodima su postojale odavno, na šta ukazuje na primer i postojanje “Puta svile”, trgovačkog puta koji je otvoren 121.g.p.n.e. i koji je spajao Kinu u zemlje na zapadu, sve do Mediterana.

Postoje i činjenice koje dokazuju da su neka otkrića u matematici potekla baš iz Kine ili da su specifična kineska, tj da se nisu pojavila ni u jednoj drugoj od navedenih civilizacija. Vreme otkrića pojedinih dostignuća u nauci jedne civilizacije može da se proceni i datiranjem arheoloških prolalazaka. Tako imamo pločice od bambusa, pronađene u Kini 1983. godine, sa “Knjigom o računanju” iz približno II veka p.n.e.
Kinezi nisu u svojim starim knjigama ostavili ni aksiome ni dokaze kakve zapadna matematika poznaje. Njihove metode su jednostavno različite od nama poznatih, ali izazivaju i divljenje i čuđenje – šta su sve i kada umeli da reše.
Dok mi mislimo da se brojanjem na prste moće stići do 10, Kinezi znaju da može i do 100000. Smatra se da su znali da sa prstima obe ruke, koristeći ovakav brojni sistem i računaju. Doduše, znamo da lako može da se množi upotrebom prstiju, od 6×6 do 10×10… zašto ne bi moglo i do 100000.
Nama možda izgleda komplikovano, međutim izgleda komplikovano i računanje njihovom specijalnom računaljkom – abakusom. Ipak, učenje na toj stvarčici je u obaveznom programu na časovima matematike u kineskim osnovnim školama, dok mnoge firme zahtevaju od svojih službenika veštinu brzog računanja na ovoj spravi, a neke domaćice ne odlaze na pijacu bez malene računaljke.
Abakus Kinezi svrstavaju među svojih pet najvećih izuma, pored papira, štamparije, kompasa i baruta, a istoričari navode da su prototipovi ove računaljke korišćeni u Kini još pre 5000 godina. Pedagozi danas u abakusu vide spravu na kojoj se osnovni matematički pojmovi uče neuporedivo bolje nego uz pomoć olovke i papira, digitrona ili kompjutera. Oni tvrde da računanje na abakusu prirodnije “aktivira mozak”. Brojevi su svuda isti, a govor drvene računaljeke je razumljiv širom sveta. Kako Kinezi tvrde, još mu nije mesto u muzeju.
Za množenje pomoću linija neki kažu da je kinesko, a neki da je modifikacija majanskog računanja. Kako god, fascinantno je u svakom slučaju.

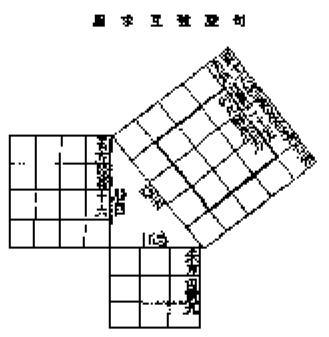
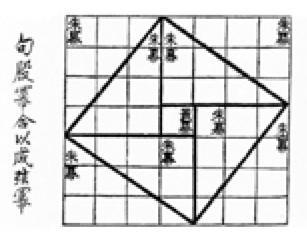 Pitagorinu teoremu, Kinezi su znali odavno. Sačuvani rukopis za koji se tvrdi da je od 1000 godina p.n.e. sadrži tekst koji govori o osobinama pravouglih trouglova. Znali su za nekoliko dokaza Pitagorine teoreme, a primenjivali su je pri rešavanju raznih zadataka. Dijagram na slici ima posebno ime – “sjuentu”, a bio je poznat pre perioda u kome je živeo Pitagora. Sisteme linearnih jednačina su rešavali šematski, a postupak je razvijen polazeći od kineske table za računanje. U njihovim zbirkama iz matematike, pronađeni su zadaci koji, na početku imaju isti broj jednačina kao i broj nepoznatih, a kasnije i onih sistema linearnih jednačina gde postoji više nepoznatih nego jednačina, uz dodatni uslov. Tu se nalaze i sistemi nelinearnih jednačina. Mi danas rešavamo zadatke po utvrđenim metodama. Oni su rešavanja davali u svakom posebnom slučaju, tako da za neke zadatke ni danas nije jasno kako su rešeni. PRIMER: Odrediti broj koji pri deljenju sa 3 daje ostatak 2, pri deljenju sa 5 ostatak 3 i pri deljenju sa 7 ostatak 2. Postupak nije komplikovan i poređaćemo sve brojeve koji zadovoljavaju redom sva tri uslova: 1. 5, 8, 11, 14, 17, 20, 23…. 2. 8, 13, 18, 23, 28,…. 3. 9, 16, 23, 30…. I naravno, u sva tri niza se 23 poklapa. Kinesko rešenje zadatka je… totalna nebuloza. Evo kako glasi: “Pri deljenju sa tri ostatak je dva, zato uzmi 140. Pri deljenju sa 5, ostatak je 3, zato uzmi 63. Pri deljenju sa 7, ostatak je 2, zato uzmi 30. Sve saberi i dobićeš 233, pa od toga oduzmi 210.” Rešenje je tačno. Ali zašto, zna samo autor.
Pitagorinu teoremu, Kinezi su znali odavno. Sačuvani rukopis za koji se tvrdi da je od 1000 godina p.n.e. sadrži tekst koji govori o osobinama pravouglih trouglova. Znali su za nekoliko dokaza Pitagorine teoreme, a primenjivali su je pri rešavanju raznih zadataka. Dijagram na slici ima posebno ime – “sjuentu”, a bio je poznat pre perioda u kome je živeo Pitagora. Sisteme linearnih jednačina su rešavali šematski, a postupak je razvijen polazeći od kineske table za računanje. U njihovim zbirkama iz matematike, pronađeni su zadaci koji, na početku imaju isti broj jednačina kao i broj nepoznatih, a kasnije i onih sistema linearnih jednačina gde postoji više nepoznatih nego jednačina, uz dodatni uslov. Tu se nalaze i sistemi nelinearnih jednačina. Mi danas rešavamo zadatke po utvrđenim metodama. Oni su rešavanja davali u svakom posebnom slučaju, tako da za neke zadatke ni danas nije jasno kako su rešeni. PRIMER: Odrediti broj koji pri deljenju sa 3 daje ostatak 2, pri deljenju sa 5 ostatak 3 i pri deljenju sa 7 ostatak 2. Postupak nije komplikovan i poređaćemo sve brojeve koji zadovoljavaju redom sva tri uslova: 1. 5, 8, 11, 14, 17, 20, 23…. 2. 8, 13, 18, 23, 28,…. 3. 9, 16, 23, 30…. I naravno, u sva tri niza se 23 poklapa. Kinesko rešenje zadatka je… totalna nebuloza. Evo kako glasi: “Pri deljenju sa tri ostatak je dva, zato uzmi 140. Pri deljenju sa 5, ostatak je 3, zato uzmi 63. Pri deljenju sa 7, ostatak je 2, zato uzmi 30. Sve saberi i dobićeš 233, pa od toga oduzmi 210.” Rešenje je tačno. Ali zašto, zna samo autor.
 Pomenuću i Paskalov trougao. Blez Paskal je živeo u 17. veku, međutim, zapis 300 godina pre njegovog rođenja pokazuje da je Kinezima itekako bilo poznato stepenovanje binoma, a samim tim i kombinatorika. Liju Hui je jedan od poznatih matematičara iz trećeg veka nove ere. Posebno je poznat po rešavanju zadataka u kojima je bilo potrebno odrediti visinu nedostupnih objekata. Takođe se zna da je, računajući površinu pravilnog mnogougla sa 3072 stranice, koji je upisan u dati krug, dobio približnu vrednost broja Pi, na 5 decimala. Njegov rezultat je bio 3.14159.
Pomenuću i Paskalov trougao. Blez Paskal je živeo u 17. veku, međutim, zapis 300 godina pre njegovog rođenja pokazuje da je Kinezima itekako bilo poznato stepenovanje binoma, a samim tim i kombinatorika. Liju Hui je jedan od poznatih matematičara iz trećeg veka nove ere. Posebno je poznat po rešavanju zadataka u kojima je bilo potrebno odrediti visinu nedostupnih objekata. Takođe se zna da je, računajući površinu pravilnog mnogougla sa 3072 stranice, koji je upisan u dati krug, dobio približnu vrednost broja Pi, na 5 decimala. Njegov rezultat je bio 3.14159.
Treba odati priznanje Kinezima što u susretu sa matematikama zapada svoju matematiku nisu u potpunosti odbacili i zamenili evropskom, tako da su se sačuvale metode iz davnina. U svakom slučaju je fascinantno pronaći u kineskim starim spisima ono za šta smo ubeđeni da je počelo sa Pitagorom ili Paskalom.